भारतीय गणितज्ञ ब्रह्मगुप्त Brahmagupta महान गणितज्ञ हैं। उन्होंने विभिन्न गणितीय सिद्धांतों का अन्वेषण किया और अपनी कृतियों के माध्यम से गणित की दुनिया में अपने अलग पहचान बनाई।
महान गणितज्ञ आचार्य ब्रह्मगुप्त का जीवन परिचय
Biography of the great mathematician Acharya Brahmagupta
प्राचीन भारत को पहले सोने की चिड़िया कहा जाता था। इसका मतलब यहाँ की संस्कृति और पुरातन ग्रंथों में लिखे शोध और ज्ञान के कारण भारत को सोने की चिड़िया कहा जाता था। प्राचीन समय से भारत में विज्ञान गणित एवं तकनीक बहुत विकसित थी। आज हम जिन बीमारियों का इलाज अभी तक ढूंढ रहे है और उन पर हर साल करोड़ो रुपये खर्च भी कर रहे हैं। ऐसी बीमारियों का इलाज आयुर्वेद से सदियों से हो रहा है।
आचार्य ब्रह्मगुप्त का प्रारम्भिक जीवन
प्राचीन भारत के महान गणितज्ञ एवं खगोल शास्त्री ब्रह्मगुप्त का जन्म 598 ईस्वी में भीनमला जो की प्राचीन गुर्जरदेश नमक प्रांत का हिस्सा था। आज के संदर्भ में देखे तो यह राजस्थान के जालौर जिले के अंतर्गत आता है। आचार्य ब्रह्मगुप्त की मृत्यु 668 ईस्वी में हुई।
आचार्य ब्रह्मगुप्त के पिता भी एक अच्छे गणितज्ञ थे। और उनका नाम जिष्णुगुप्त था। गणित की प्रारंभिक शिक्षा उन्हें अपने पिता से मिली जिसके कारण उनका रुझान गणित और खगोल की तरफ बढ़ा। ब्रह्मगुप्त कितने प्रखंड विद्वान थे। इसका अंदाजा इसी बात से लगाया जा सकता है कि उन्होंने मात्र 30 वर्ष की आयु में ब्रह्मस्पुट सिद्धान्त Brahmagupta theory जैसे महान ग्रंथ की रचना की।
आचार्य ब्रह्मगुप्त ब्रह्मरक्ष परंपरा के अनुयायी थे। यह एक जानी-मानी ज्ञान परंपरा थी। जिसमें बहुत बड़े-बड़े विद्वान वाद-विवाद एवं शोध करते थे। ज्योतिष में गहरी दिलचस्पी होने के कारण उन्होने ग्रहण, तारों, सूर्य, सौर मण्डल आदि के बारे में गहन अध्ययन किया। वो भी बिना किसी आधुनिक संसाधन के जैसा की आज के समय मौजूद हैं।
आचार्य ब्रह्मगुप्त के महत्वपूर्ण तथ्य एक नजर में
पाई के सटीक मान की गणना प्रस्तुत की।
शून्य की विभिन्न गणितीय संक्रिया प्रस्तुत की।
sin और cos पर काम कर त्रिकोणमिती को आगे बढ़ाया।
अनंत और शून्य पर काम कर कैलकुलस के लिए नीव रखी।
पृथ्वी की परिधि की गणना कर बताया की इसकी परिधि 36000 किमी हैं।
गुरुत्वाकर्षण की संकल्पना प्रस्तुत की।
पृथ्वी की घूर्णन अवधि 365 दिन, 6 घंटे, 12 मिनट, 36 सेकेंड में पूरी होती हैं
चन्द्रग्रहण, सूर्यग्रहण की व्याख्या की।
आचार्य ब्रह्मगुप्त द्वारा लिखित ग्रंथ हैं- ब्रह्मस्पुट सिद्धान्त, कंजीका, मोहसाधन
पाई के सटीक मान की गणना
पाई (pi) π का मान निकालना शुरू से ही गणितज्ञों के लिए एक कठिन कार्य रहा लेकिन ब्रह्मगुप्त ने पाई (pi) π का मान भी दिया जो 20 के वर्गमूल के 3.16227766 अंकों तक समान है। आज भी विद्वान उनकी इस गणना के लिए उनको याद करते हैं।
शून्य के साथ धनात्मक एवं ऋणात्मक अंको की विभिन्न गणितीय संक्रिया
ऋणात्मक संख्या में से शून्य को घटाने पर ऋणात्मक संख्या मिलेगी। जैसे -100 – 0 = -100
धनात्मक संख्या में से शून्य घटाने पर धनात्मक संख्या मिलेगी। जैसे 100 + 0 = 100
शून्य में से अगर शून्य को घटा दिया जाए तो शून्य प्राप्त होगा। जैसे 0-0=0
शून्य में से अगर ऋणात्मक सख्या घटायी जाए तो धनात्मक संख्या मिलेगी। जैसे 0-(-100) = 100
यदि शून्य से घटाया गया धनात्मक संख्या है तो परिणाम ऋणात्मक संख्या होगी।
ऋणात्मक संख्या या धनात्मक संख्या से शून्य का गुणा करने पर गुणनफल शून्य प्राप्त होगा।
शून्य का शून्य से गुणा करने पर गुणनफल शून्य प्राप्त होगा।
ऋणात्मक संख्या और धनात्मक संख्या का गुणनफल या भागफल ऋणात्मक संख्या प्राप्त होगा
त्रिकोणमिती Trigonometry के क्षेत्र में काम
त्रिकोणमिती Trigonometry के क्षेत्र में ब्रह्मगुप्त नें sin table यानि ज्या सारणी तैयार किया। जिसमें sin के विभिन्न मानों को निकाला और एक अच्छी सारणी का रूप दिया।
इसके अलावा पहाड़ की ऊँचाई को निकालने तथा चोटी तक पहुँचने में चली गयी दूरी की गणना का प्रयास किया। इस प्रकार देखा जाए तो ब्रह्मगुप्त त्रिकोणमिती में काफी काम किया।
रेखीय समीकरण का हल
आचार्य ब्रह्मगुप्त के समय रेखीय समीकरण पर आधारित समस्या को हल करने के लिए कोई भी तरीका मौजूद नहीं था। ऐसे समय में जब सरल रेखीय समीकरण को हल करना एक कठिन कार्य माना जाता था। ब्रह्मगुप्त ने अपनी विद्वता का परिचय देते हुये रेखीय समीकरण को हल करने की विधि सबकी समक्ष प्रस्तुत की जो आज भी प्रचलित हैं।
द्विघात समीकरण का हल
ब्रह्मगुप्त नें द्विघात समीकरण को करने के लिए एक आसान सा सूत्र प्रस्तुत किया जिसकी सहायता से कठिन से कठिन समीकरण को हल करना आसान हो गया। आप में से काफी लोग इस सूत्र से काफी हद तक परिचित होंगे।
जो क्रमशः समीकरण ax 2 + bx = c के लिए हल हैं,
![]()
जैसा की हम जानते हैं द्विघात समीकरण में हमें x के क्रमशः दो मान प्राप्त होता हैं।
प्रथम n प्रकृतिक संख्या के वर्गो का योग
जैसा की हम जानते हैं। अगर कोई ऐसी श्रेणी हमारे सामने आ जाए जो काफी लंबी हो तो उसको हल करने में बहुत सारा समय नष्ट न हो इसके लिए हमें किसी सूत्र की जरूरत थी इसी समस्या के समाधान के लिए ब्रह्मगुप्त नें एक सूत्र प्रस्तुत किया।
12+22+32+42+52+……..+n2
प्रथम n प्रकृतिक संख्या के वर्गो का योग= n(n+1)(2n+1)/6
इस समीकरण द्वारा हम कितनी भी लंबी श्रंखला न हो आसानी से हल कर सकते हैं।
प्रथम n प्रकृतिक संख्या के घनों का योग
ब्रह्मगुप्त नें प्रकृतिक संख्या के घनों का योग ज्ञात करने के लिए एक सूत्र प्रस्तुत किया जिसके माध्यम से बड़ी से बड़ी श्रंखला का योग आसान हो गया।
प्रथम n प्रकृतिक संख्या के घनों का योग= 13 + 23 + 33 + 43 + … + n3
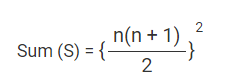
पृथ्वी के आकार का सही अनुमान लगाया
आचार्य ब्रह्मगुप्त नें आज से हजारो साल पहले ही बता दिया था की पृथ्वी की सतह छपती न होकर गोल हैं। आज से 1400 साल पुरानी धार्मिक पुस्तक में तो इस बात पर ज़ोर देके कहा गया था की पृथ्वी गोल हैं। शुरुआत में लोगो को इस बात को समझने में कठिनाई हुई पर बाद में लोगो के द्वारा इसे मान्यता मिल गयी। बाद में आधुनिक वैज्ञानिकों नें भी इस बात को सही माना कि पृथ्वी गोल है ।
गुरुत्वाकर्षण की संकल्पना
आचार्य ब्रह्मगुप्त नें बताया की पृथ्वी पर हर जगह कोई एक ऐसी शक्ति काम कर रही हैं। जो स्वाभाविक रूप से हर एक पिंड पर लग रही हैं। जिसके कारण ही बारिश की बूंदें और वृक्षों के पत्ते और फल नीचे गिरते हैं। आप जानते हैं की इस बात को यूरोप के एक वैज्ञानिक नें सकड़ों साल बाद दुनियाँ के सामने लाया। जिनका नाम न्यूटन था।
पृथ्वी के घूर्णन की अवधि Period of rotation of the earth
आचार्य ब्रह्मगुप्त नें ग्रहों की गति पर काफी शोध किया और बहुत सारी जानकारी दुनिया के सामने लायी जिसमें से एक था पृथ्वी के घूर्णन की अवधि । हमारी पृथ्वी कितने दिन में सूर्य का चक्कर लगा लेती हैं। और इसकी काफी गणना के बाद एक निष्कर्ष सामने प्रस्तुत किया की हमारी पृथ्वी 365 दिन, 6 घंटे, 12 मिनट, 36 सेकेंड में सूर्य का पूरा चक्कर कर लेती हैं।
आचार्य ब्रह्मगुप्त की प्रमुख पुस्तकें
1- ब्रह्मस्पुत सिद्धान्त
ब्रह्मस्पुत सिद्धान्त आचार्य ब्रह्मगुप्त की महत्वपूर्ण कृति है, जिसकी रचना लगभग 628 ईस्वी में हुई। जिसमें अद्वितीय भारतीय गणितीय सिद्धांतों का प्रतिपादन किया गया है। इसमें संपूर्ण संख्या प्रणाली की कई प्रकारों पर चर्चा की गई है। यह सूत्रों का संग्रह है जो गणितीय प्रश्नों के समाधान में मदद करते हैं। इस ग्रंथ में उन्होंने शून्य को एक अलग तरह से उल्लेख किया है और शून्य तथा ऋणात्मक अंकों से संबंधित प्रश्नों को हल करने के नियम दिए है।
2- कंजीका
आचार्य ब्रह्मगुप्त की दूसरी महत्वपूर्ण कृति है जिसमें अलग-अलग विषयों में गणित की विस्तृत जानकारी दी गई है। इसमें आलेख, छंद और ज्योतिषशास्त्र के अध्ययन के साथ-साथ सभी प्रमुख गणितीय संबंधित विषयों पर चर्चा की गई है।
3- मोहसाधन
आचार्य ब्रह्मगुप्त ने अपनी यह तीसरी कृति में बीज गणित के विभिन्न पहलुओं पर ज्ञान का प्रस्तावना किया है। इसमें भिन्न-भिन्न प्रकार के समीकरणों के समाधान उपलब्ध हैं और उन्होंने बीज गणित की महत्वपूर्णता को दर्शाया है।आचार्य ब्रह्मगुप्त की यह महत्वपूर्ण कृतियाँ हमें उनके गणितीय दृष्टिकोण और सिद्धांतों का अवलोकन करने में मदद करती हैं। उनकी योगदान के कारण हमारे महान गणितज्ञ आज भी उन्हें याद करते हैं और उनकी कृतियों का अध्ययन करते हैं। ऐसे ही देशभक्ति, धैर्य और क्रियाशीलता के साथ ब्रह्मगुप्त ने गणित के क्षेत्र में सर्वश्रेष्ठ गणितज्ञों में अपनी जगह बनाई।
आचार्य ब्रह्मगुप्त चक्रीय चतुर्भुज के क्षेत्रफल का सूत्र प्रदान करने वाले दुनिया के पहले गणितज्ञ थे। आप उज्जैन जो की वर्तमान मध्य प्रदेश में स्थित हैं के अन्तरिक्ष प्रयोगशाला के प्रमुख थे। आप ने खगोल विज्ञान की पढ़ाई के लिए में ब्रह्मपक्ष स्कूल (गुर्जरदेश) में दाखिला लिया। हम सब जो सूत्र त्रिभुज का क्षेत्रफल निकालने के लिए करते है जिसको हेरोन का सूत्र कहते है वो भी सदियों पहले आचार्य ब्रह्मगुप्त ने ही दिया।
{A= √ s(a-b)(b-c)(c-a)}
आचार्य ब्रह्मगुप्त एक ओजस्वी संप्रदाय से संबंधित थे, जो कि ज्योतिष, संख्या और छाया चित्रण की कला और आदर्शों के प्रतिपादन को प्रचारित करते है।




